Overview and Objective
In this lesson, students will created string are designs while exploring the maximum number of intersection points and regions of any number of lines intersecting in a plane.
Warm-Up
Start by discussing the following questions with students:
- If two lines intersect in a plane, in how many points do they intersect?

- If three lines intersect in a plane, in how many points do they intersect? Encourage them to come up with different answers. Invite them to share their drawings with the whole class.
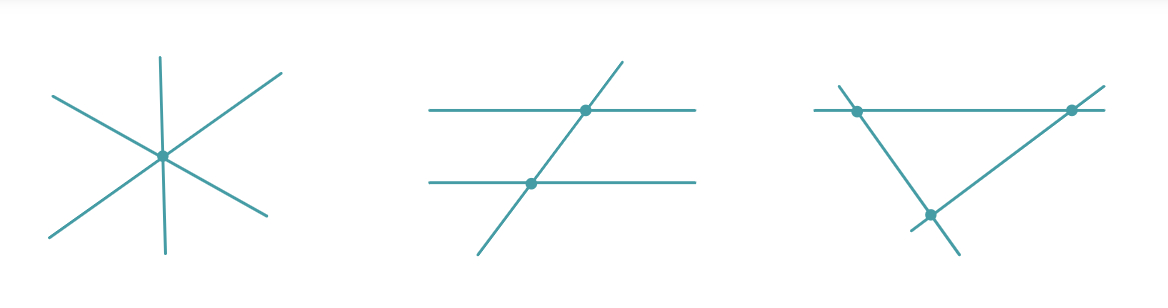
Now, ask students to explore four lines. Allow students some time to work on a blank Polypad to show all possible answers.
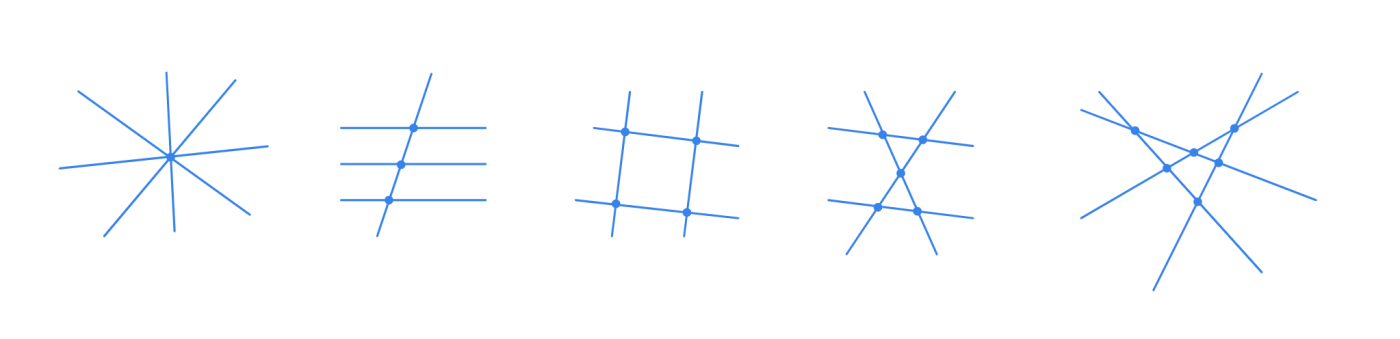
Again, they will come up with different answers. Students can find an example of lines intersecting in 0, 1, 3, 4, 5, and 6 points. All but 2. Clarify with the students that, there isn't any way for four lines to intersect in two points. The minimum number of intersection points for any number of lines is always 1 whereas the maximum number of intersection points seems to change with the number of lines. But how?
Main Activity
Ask students the maximum number of intersection points and regions of 20 coplanar lines. Encourage them to work systematically by sharing this canvas. They can use the table tool to record their findings.
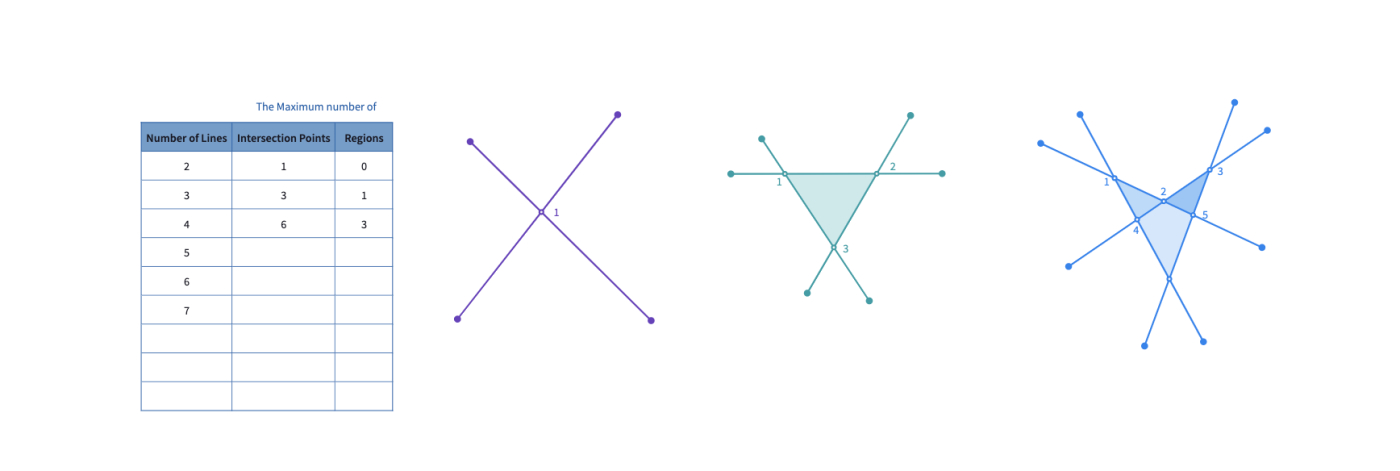
https://mathigon.org/polypad/8pmFdyWjFh8igA
After they come up with the drawings and answers, let them share their strategies to find the maximum number of intersection points and regions. Some possible drawings and answers are shown on this canvas.
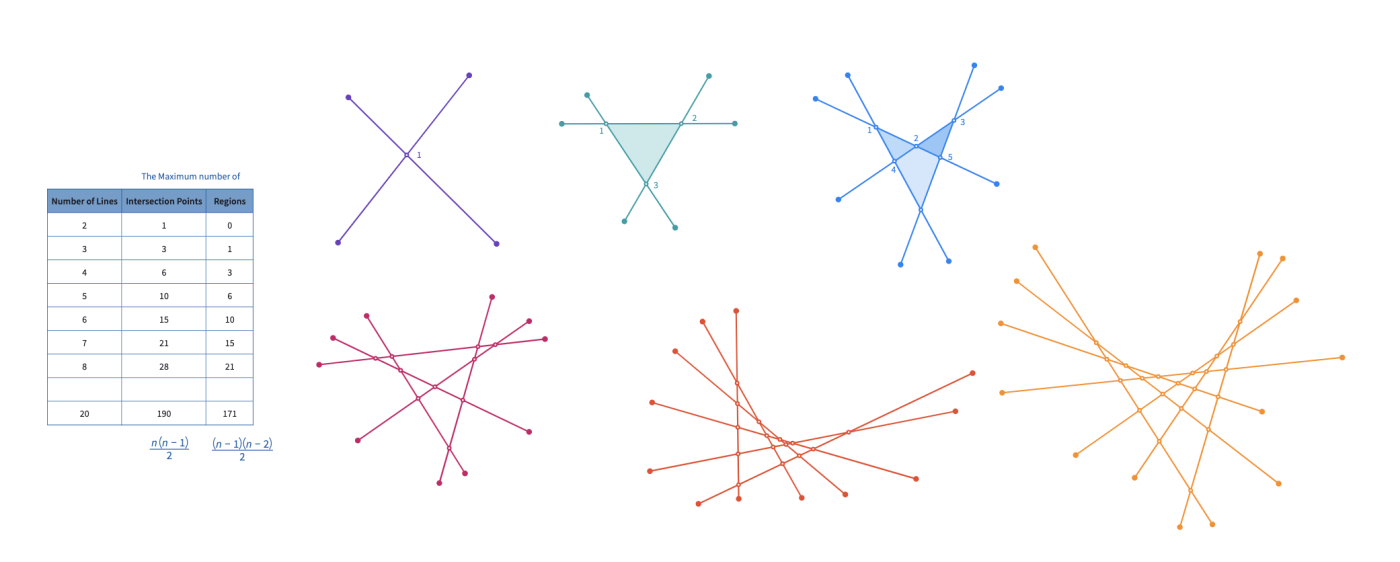
It gets harder to see the regions and the intersection points as the number of lines increases, so to solve this difficulty we can use some artistic designs called string art or curve stitching.
You may use the dotted grids, number line, or the coordinate plane to start with. Here is an example of using the number lines and straight-line drawing tool to create 5 intersecting lines.
We use two number lines as the template and draw the lines like a sliding ladder so that they intersect each other in a maximum number of points. When you erase the number lines, the remaining shape clearly shows you the regions and points.
Ask how many intersection points are added each time a new line is added to the previous shape. This discussion leads to the discovery of triangular numbers as the pattern for finding the maximum number of points and regions.
Discuss the benefits of using this method in drawing the intersecting lines. It helps to count the regions and points systematically as well as shows the reason behind the triangular numbers.
Closure
Share this canvas of the string art templates with the class. Invite students to create their own string art designs. You may want to show this video to students for possible examples.
To close the lesson, share some student work with the class by discussing how art can help to find the solutions to some mathematical problems. You may also ask for examples of how math helps art to find solutions. Both math and art are based on the understanding of shapes, symmetry, proportion, and measurement. They both require spatial reasoning skills, creativity, the ability to recognize patterns, and imagination. There are endless ways in which art and math overlap to solve problems and create new designs.
Support and Extension
For students ready for additional extension in this lesson, consider asking questions about the congruent regions in each string art design. They can start creating the regions and use the flip option to create the symmetric tiles of the design.
Polypads for This Lesson
To assign these to your classes in Mathigon, save a copy to your Mathigon account. Click here to learn how to share Polypads with students and how to view their work.