Polygons and PolyhedraTessellations

Polygons appear everywhere in nature. They are especially useful if you want to tile a large area, because you can fit polygons together without any gaps or overlaps. Patterns like that are called tessellations.

honeycomb

Sinaloan Milk Snake skin

Cellular structure of leafs

Basalt columns at Giant’s Causeway in Northern Ireland

Pineapple skin

Shell of a tortoise

Humans have copied many of these natural patterns in art, architecture and technology – from ancient Rome to the present. Here are a few examples:

pavement pattern

Greenhouse at the Eden Project in England

Mosaic at Alhambra

roof at the British Museum in London

Cellular tessellation pavilion in Sydney

Study of Regular Division of the Plane with Reptiles, M. C. Escher

Here you can create your own tessellations using regular polygons. Simply drag new shapes from the sidebar onto the canvas. Which shapes tessellate well? Are there any shapes that don’t tessellate at all? Try to create interesting patterns!

Examples of other students’ tessellations

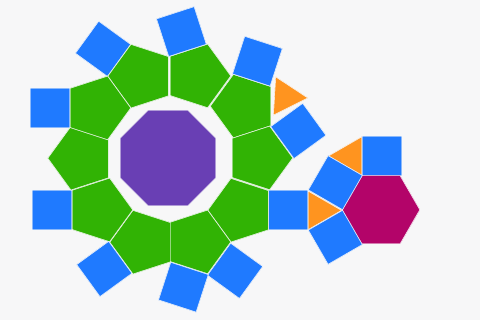
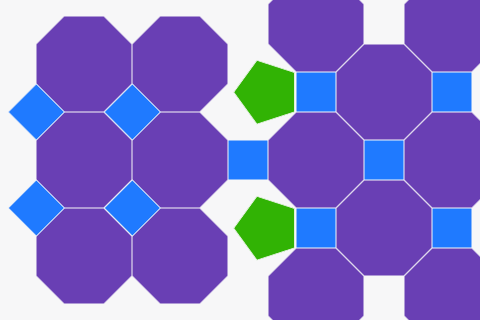
Tessellations from regular polygons

You might have noticed that some regular polygons (like ) tessellate very easily, while others (like ) don’t seem to tessellate at all.

This has to do with the size of their internal angles, which we learned to calculate before. At every vertex in the tessellation, the internal angles of multiple different polygons meet. We need all of these angles to add up to °, otherwise there will either be a gap or an overlap.

Triangles because 6 × 60° = 360°.

Squares because 4 × 90° = 360°.

Pentagons because multiples of 108° don’t add up to 360°.

Hexagons because 3 × 120° = 360°.

You can similarly check that, just like pentagons, any regular polygon with 7 or more sides doesn’t tessellate. This means that the only regular polygons that tessellate are triangles, squares and hexagons!

Of course you could combine different kinds of regular polygons in a tessellation, provided that their internal angles can add up to 360°:

Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°

Hexagons and triangles
120° + 120° + 60° + 60° = 360°

Hexagons and triangles
120° + 60° + 60° + 60° + 60° = 360°

Hexagons, squares and triangles
120° + 90° + 90° + 60° = 360°

Octagons and squares
135° + 135° + 90° = 360°

Dodecagons (12-gons) and triangles
150° + 150° + 60° = 360°

Dodecagons, hexagons and squares
150° + 120° + 90° = 360°

Tessellations from irregular polygons

We can also try making tessellations out of irregular polygons – as long as we are careful when rotating and arranging them.

It turns out that you can tessellate not just equilateral triangles, but any triangle! Try moving the vertices in this diagram.

The sum of the internal angles in a triangle is °. If we use each angle at every vertex in the tessellation, we get 360°:

More surprisingly, any quadrilateral also tessellates! Their internal angle sum is °, so if we use each angle at every vertex in the tessellation, we we get 360°.

Pentagons are a bit trickier. We already saw that regular pentagons , but what about non-regular ones?

Here are three different examples of tessellations with pentagons. They are not regular, but they are perfectly valid 5-sided polygons:

Over time, mathematicians have only found 15 different kinds of tessellations with (convex) pentagons – the most recent of which was discovered in 2015.

Two years later, in 2017, Michaël Rao published a proof that there are no other possibilities, except the 15 that had already been found. Can you make a tessellation using all of them?

Shapes provided by the Math Happens Foundation

Tessellations in Art

Many artists, architects and designers use tessellations in their work. One of the most famous examples is the Dutch artist M. C. Escher. His works contain strange, mutating creatures, patterns and landscapes:

“Sky and Water I” (1938)

“Lizard” (1942)

“Lizard, Fish, Bat” (1952)

“Butterfly” (1948)

“Two Fish” (1942)

“Shells and Starfish” (1941)

These artworks often look fun and effortless, but the underlying mathematical principles are the same as before: angles, rotations, translations and polygons. If the maths isn’t right, the tessellation is not going to work!

“Metamorphosis II” by M. C. Escher (1940)

Penrose Tilings

All the tessellations we saw so far have one thing in common: they are periodic. That means they consist of a regular pattern that is repeated again and again. They can continue forever in all directions and they will look the same everywhere.

In the 1970s, the British mathematician and physicist Roger Penrose discovered non-periodic tessellations – they still continue infinitely in all directions, but never look exactly the same. These are called Penrose tilings, and you only need a few different kinds of polygons to create one:

Move the slider to reveal the underlying structure of this tessellation. Notice how the same patterns appear at various scales: the yellow pentagons, blue stars, purple rhombi and green ‘ships’ appear in their original size, in a slightly larger size and an even larger size. This self-similarity can be used to prove that a Penrose tiling is always non-periodic.

Penrose was exploring tessellations purely for fun, but it turns out that the internal structure of some real materials (like aluminium) follow a similar pattern. The pattern was even used on toilet paper, because the manufacturers noticed that a non-periodic pattern can be rolled up without any bulges.

Змінити мову

Увійдіть до Mathigon

Поділіться

Скинути прогрес